如何实现浏览器的前进和后退功能
如何理解“栈”?
- 后进者先出,先进者后出的数据结构
- 栈是一种 操作受限 的线性表
如何实现一个“栈”
- 栈主要包括两个操作,入栈和出栈
- 顺序栈:用数组实现的栈
- 链式栈:用链表实现
支持动态扩容的顺序栈
顺序栈
- 逻辑
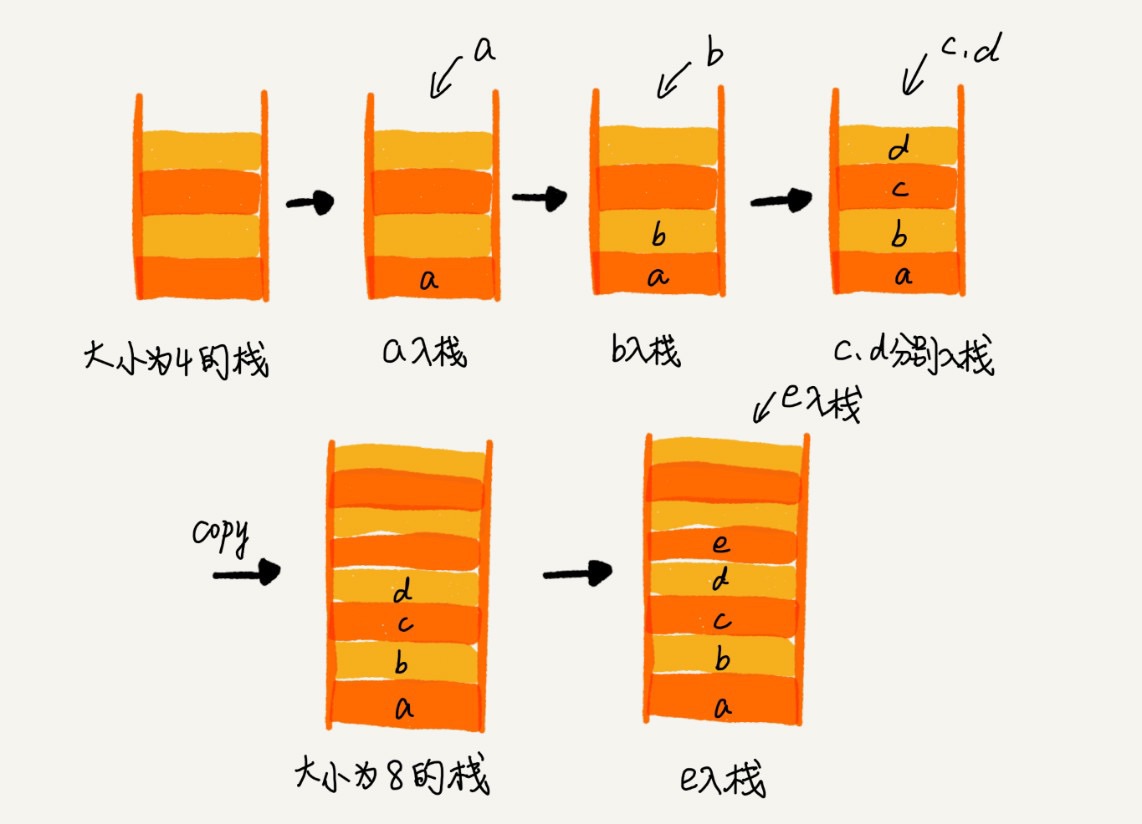
- 时间复杂度
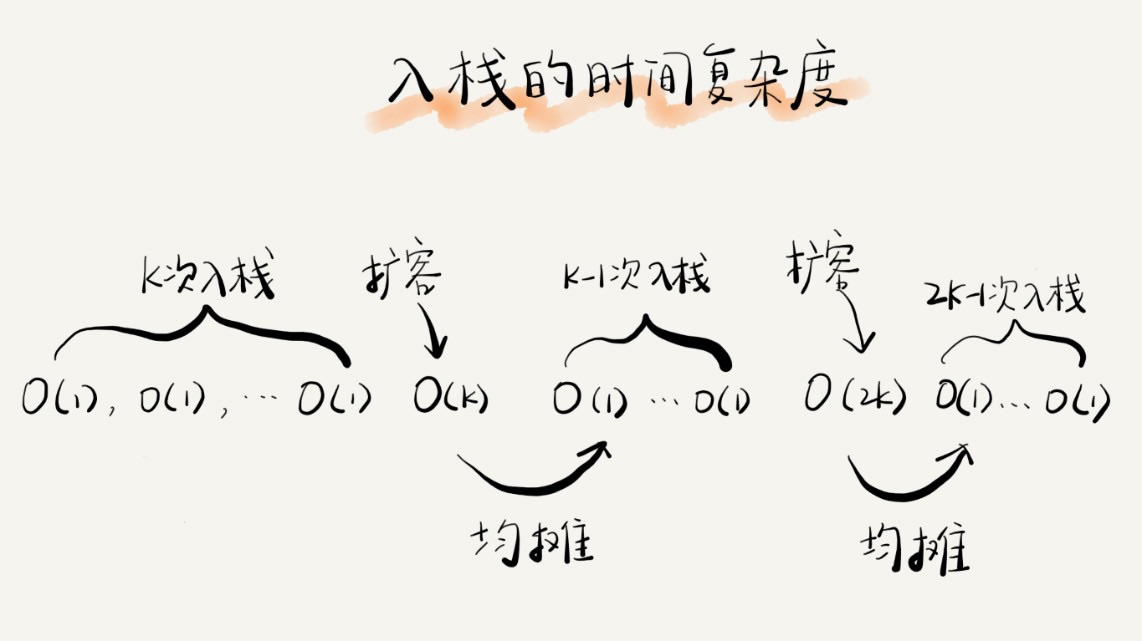
- 逻辑
一般使用链式栈来实现可动态扩容的栈
栈的应用
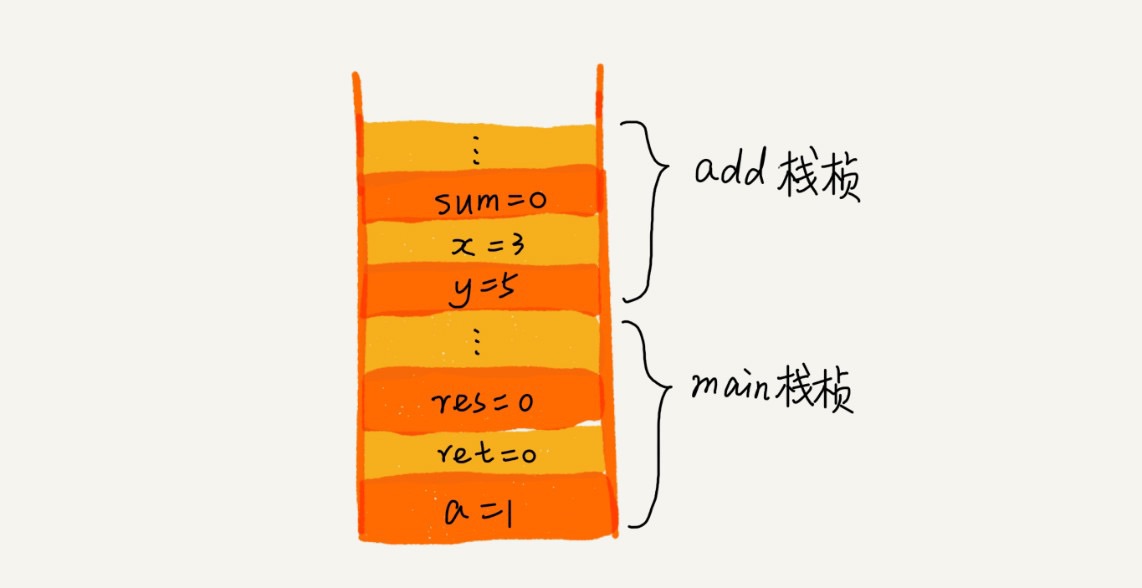
栈在函数调用中的应用
- 操作系统给每个线程分配一个独立的内存空间,这块内存使用 栈 的数据结构
- 进入函数,将临时变量入栈
- 当被调用函数执行完成,返回之后,函数对应的栈帧出栈
int main() {
int a = 1;
int ret = 0;
int res = 0;
ret = add(3, 5);
res = a + ret;
printf("%d", res);
return 0;
}
int add(int x, int y) {
int sum = 0;
sum = x + y;
return sum;
}
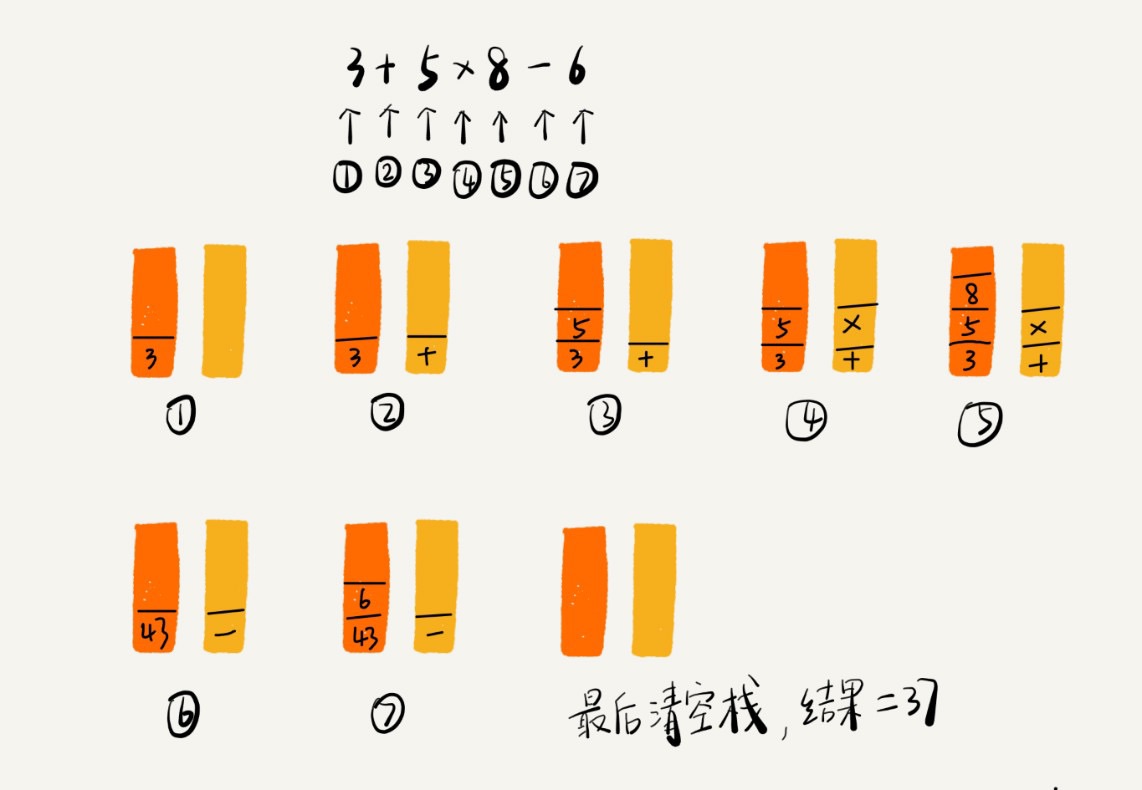
栈在表达式求值中的应用
- 用两个栈来实现,一个保持操作数的栈, 另一个保存运算符的栈
- 从左向右遍历表达式, 当数字,直接压入操作数栈,当遇到运算符,与操作符栈的栈顶元素进行比较
- 如果运算符栈顶元素优先级高,就将当前运算符压入栈
- 如果比运算符栈顶元素的优先级低或相同,从运算符栈中取栈顶运算符,从操作数的栈顶取2个操作数,进行计算,再把计算结果压入操作数栈中
- 继续比较
栈在括号匹配中的应用
- 遇到左括号将其压入栈
- 遇到右括号,取出栈顶元素比较
- 匹配则继续,否则返回错误
解答开篇
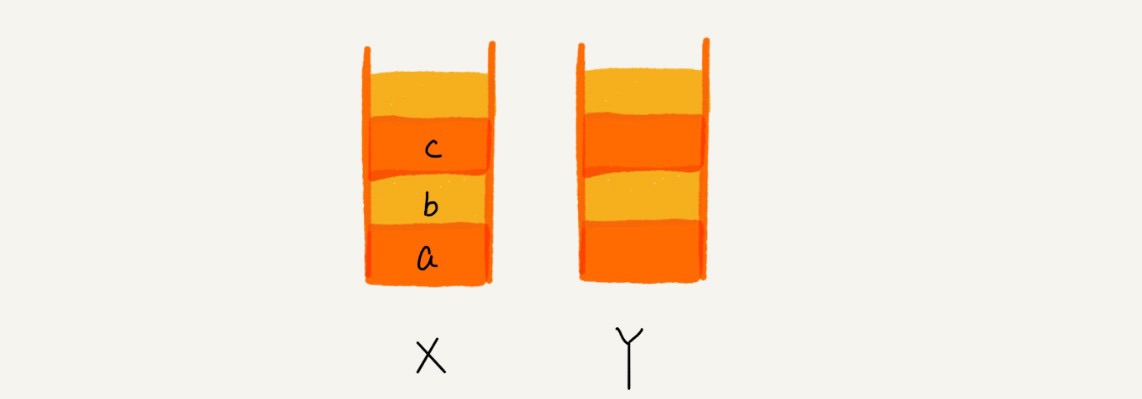
- 两个栈 X 和 Y
- 前进从 Y 到 X
- 后退从 X 到 Y
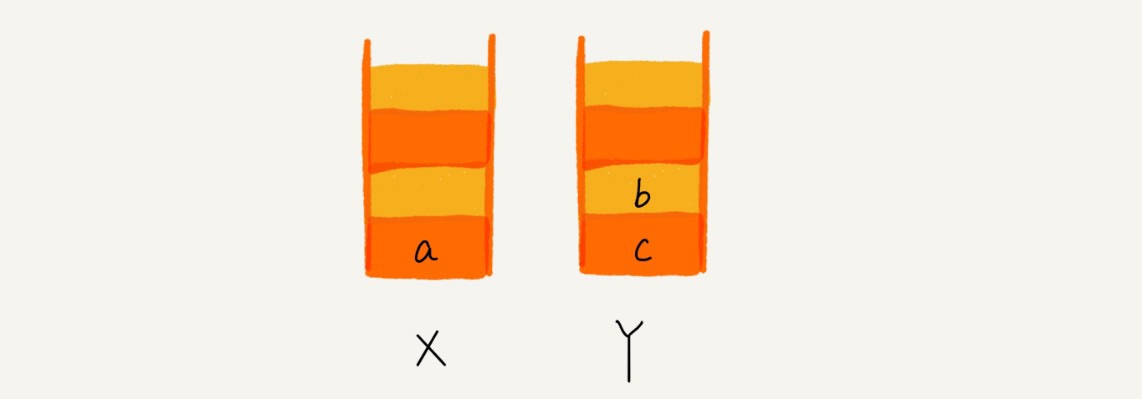
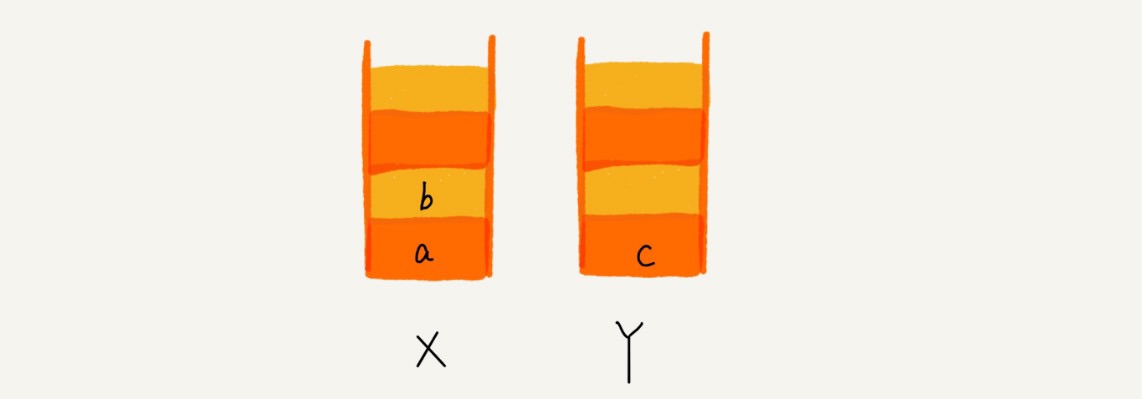
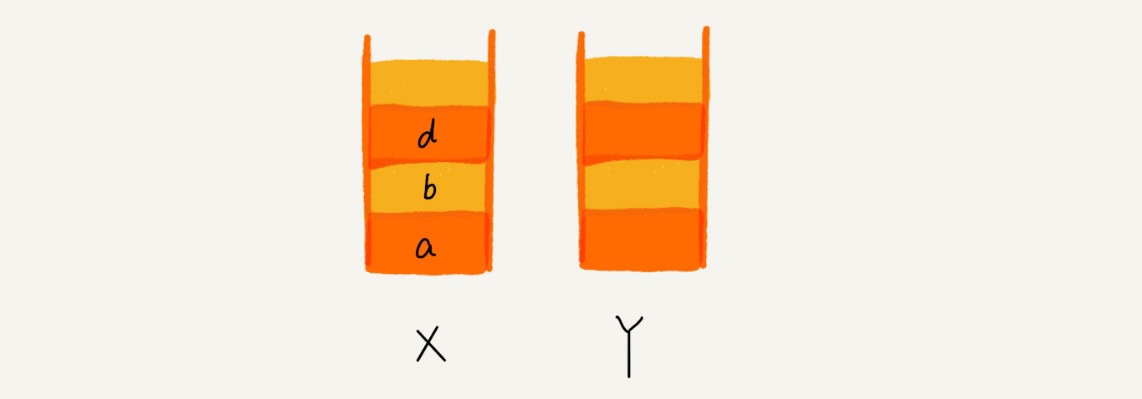
总结
- 后进先出
- 只这次入栈和出栈
- 链式栈 出栈 入栈 时间复杂度为O(1)
- 顺序栈 出栈 时间复杂度为O(1),入栈 均摊复杂度为O(1)
- 一般均摊复杂度 和 最好情况时间复杂度相同,因为将最坏情况均摊后,一般都和最好差不多
