导语：给定一个用户ID， 如何查找这个用户的“最终推荐人”？

如何理解“递归”

问题

问： 看电影时想知道自己在第几排？
答： 问前一排，前一排再问前一排，直到问到第一排，再返回每一排位置，最终得到结果
解析： 去的过程叫“递”， 回来的过程叫“归”

递推公式

  1. 基本上，所有的递归问题都可以用递推公式来表示
f(n) = f(n - 1) + 1,  其中 f(1) = 1

代码实现

int f(int n)
{
	if(n == 1) return 1;
	return f(n-1) + 1;
}

递归需要满足的三个条件

  1. 一个问题的解可以分解为几个子问题(数据规模更小)的解

  2. 分解后的子问题，除了数据规模不同，求解思路完全相同

  3. 存在递归终止条件

如何编写递归代码

问题

n个台阶，每次你可以跨1个台阶或2个台阶，n个台阶有多少种走法？

方法

写出递归公式，找到终止条件

f(1) = 1;
f(2) = 2;
f(n) = f(n-2) + f(n-1);

代码实现

int f(int n)
{
	if(n == 1) return 1;
	if (n == 2) return 2;
	return f(n-1) + f(n);
}

总结

  1. 将大问题分解为小问题的规律
  2. 写出递推公式
  3. 确定终止条件
  4. 将递推公式和终止条件翻译成代码

递归代码要警惕堆栈溢出

  1. 函数调用使用栈保存临时变量
  2. 函数执行完成返回时出栈
  3. 一直压入栈，会有堆栈溢出风险

如何避免出现堆栈溢出

  1. 限制递归深度
    int f(int n){
	++depth;
	if (depth > 1000) {
		throw exception;
	}

	if (n == 1) return 1;
	return f(n-1) + 1;
}
  2. 缺点：站空间无法确定，递归深度不可靠

递归代码要警惕重复计算

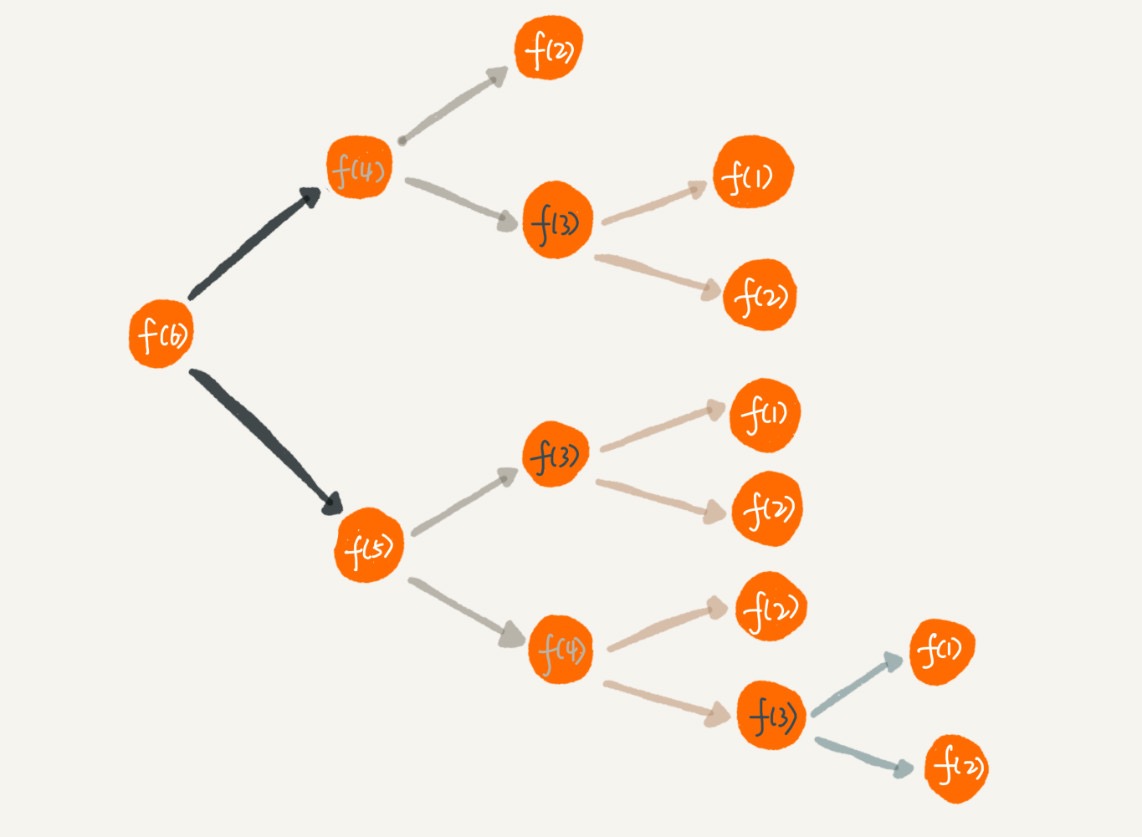
recursion1

通过一个数据结构（比如散列表）来保存已经求解的结果f(k)

public int f(int n){
	if (n == 1) return 1;
	if (n == 2) return 2;

	if (hasSolvedList.containsKey(n)) {
		return hasSolvedList.get(n);
	}

	int ret = f(n-1) + f(n-2);
	hasSolvedList.put(n, ret);
	return ret;
}

时间复杂度：

  1. O(n)
  2. 无法确定，因为函数调用会有额外开销

空间复杂度:

  1. O(n)，在递归结束之前，所有函数的变量都会被保存，所以空间复杂度为O(n)

递归代码改写非递归代码

Exapmle1

int f(int n)
{
	if(n == 1) return 1;
	return f(n-1) + 1;
}

等价于

int f(int n)
{
	int ret = 1;
	for (int i = 2; i <= n; i++) {
		ret = ret + 1;
	}
	return ret;
}

Exapmle2

int f(int n)
{
	if(n == 1) return 1;
	if (n == 2) return 2;
	return f(n-1) + f(n);
}

等价于

int f(int n) {
	if (n == 1) return 1;
	if (n == 2) return 2;

	int ret = 0
	int pre = 2;
	int prepre = 1;

	for (int i = 3; i <= n; i++) {
		ret = pre + prepre;
		prepre = pre;
		pre = ret;
	}

	return ret;
}

递归调试方式

  1. 打印日志发现递归值
  2. 结合条件断点调试

解答开篇

如何找到最终推荐人

long findRootReferererId(long actorId) {
	Long referrerId = select refrerrer_id from [table] where actor_id = actorId;
	return findRootReferererId(referrerId);
}

存在问题

  1. 递归深度未知
  2. 无限递归 (A-B-C-A)

总结

  1. 满足三个条件即可递归
    1. 可拆分
    2. 可重复
    3. 有终止
  2. 递归三步骤
    1. 写出递归公式
    2. 找出终止条件
    3. 翻译递归代码
  3. 递归弊端
    1. 堆栈溢出
    2. 重复计算
    3. 函数调用耗时多
    4. 空间复杂度高
      …

扩展

斐波那契数列（Fibonacci sequence）

  1. 定义

    这个数列从第3项开始，每一项都等于前两项之和

  2. 实现

    1. 写出递归公式
      f(n) = f(n-2) + f(n-1);
    2. 终止条件
      f(0) = 0;
f(1) = 1;
    3. 翻译递归代码
      int Fibonacci(n){
	if (n == 0) return 0;
	if (n == 1) return 1;

	//在return时打印即可打印所有数列
	return f(n-2) + f(n-1);
}

详见: 黄铮的 数据结构与算法之美 课程系列