上篇中的常见复杂度分析O(1)、O(logn)、O(n)、O(nlogn)外，还有更细致的分析方法

4种更细致的时间复杂度方法

  1. 最好情况时间复杂度（best cast time complexity）
  2. 最坏情况时间复杂度 (worst case time complexity)
  3. 平均情况时间复杂度 (average case time complexity)
  4. 均摊时间复杂度 (amortized time complexity)

最好、最坏情况时间复杂度

int find(int[] array, int n, int x)
{
	int i = 0;
	int pos = -1;
	for (; i < n; i++)
	{
		if (array[i] == x) {
			pos = i;
			break;
		}
	}
	return pos;
}
  1. 这段代码与之前不同的地方在于，它的时间复杂度不单单取决于n，还取决于x的值
  2. 最好情况下，只需要查找一次即可，所以最好情况时间复杂度为O(1)
  3. 最坏情况下，需要搜索数组所有元素，所以最坏情况复杂度为O(n)
  4. 所以这个算法，不能单单说时间复杂度为O(1) 或 O(n)

平均情况时间复杂度

  1. 绝对平均值
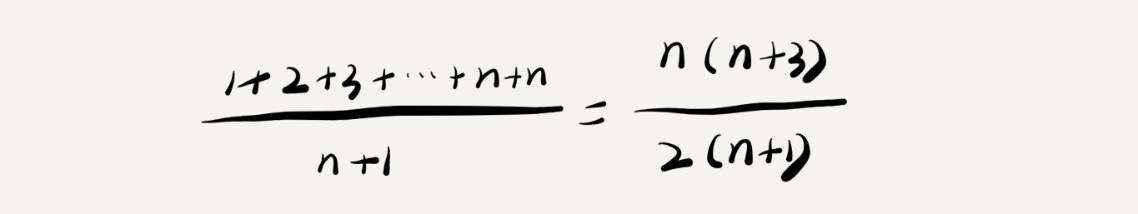
    image

  2. 期望平均值（加权平均值）
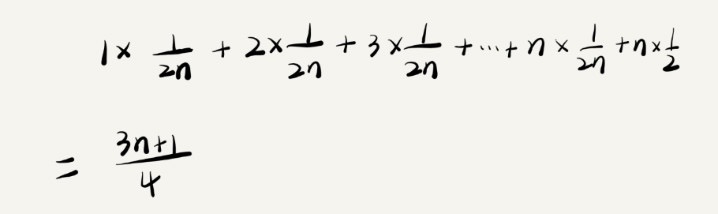
    image

    1. 在数组内的概率为1/2
    2. 0到n-1中任意位置的概率为1/(2n)

  3. 绝对平局值和期望平均值的时间复杂度都为O(n),但还是有区别

  4. 一般我们指的平均时间复杂度是指期望平均值

均摊时间复杂度

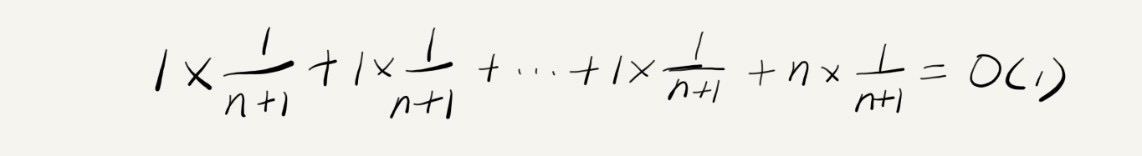
image

  1. 每种情况的时间复杂度O(1)
  2. 将n+1种情况发生的概率1/(n+1)相加
  3. 均摊时间复杂度为O(1)
  4. 由于平均时间复杂度计算太过细致，可以使用均摊时间复杂度来计算