复杂度分析上

数据结构和算法本身解决的是执行效率（“快”和“省”）的问题，考量执行效率的指标就是复杂度分析。复杂度分析主要由时间复杂度和空间复杂度组成。

为什么需要复杂度分析

性能测试（事后统计法）局限性

1. 测试结果非常依赖测试环境
2. 测试结果受数据规模的影响很大

大O复杂度表示法

T(n) = O(f(n))

1. 并不具体表示代码真正的执行时间
2. 表示代码执行时间随数据规模增大的变化趋势
3. 也叫作渐进时间复杂度（asymptotic time complexity）
4. 简称时间复杂度

时间复杂度分析

1. 只关注循环执行次数最多的一段代码
2. 加法法则：总复杂度等于量级最大的那段代码的复杂度
3. 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

常见的复杂度分析实例分析

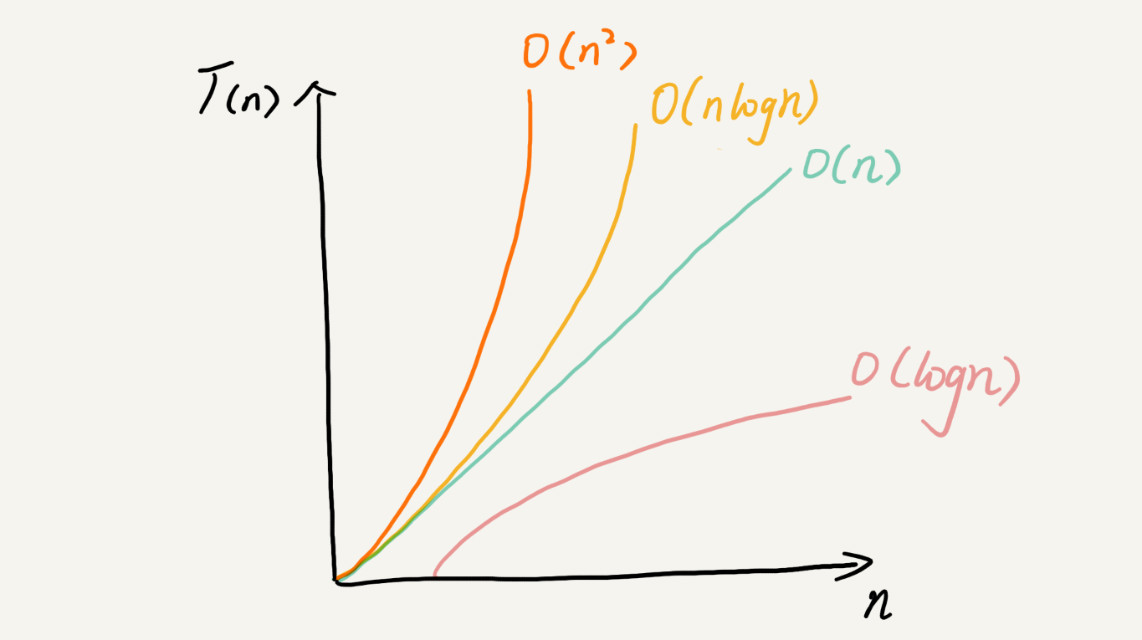
复杂度量级（按数量级递增）

复杂度分为两类

1. 多项式量级
2. 非多项式量级
   1. 非多项式量级问题叫作NP（Non-Deterministic Polynomial， 非多项式）问题
   2. 当数据规模n越来越大时，执行时间会急剧增加
   3. 指数阶 和 阶乘阶 为非多项式量级

多项式量级

O(1)

1. 常量级时间复杂度
2. 执行时间与数据规模n无关

O(logn)、O(nlogn)

代码

i = 1
while (i <= n) {
	i = i + 2;
}

分析

$$x = \log_2n => logn $$

O(m+n)、O(m*n)

1. 当m 和 n 不知道谁的规模大时，为O(m+n)
2. 当m 和 n 不知道谁的规模大时，为O(m*n)

空间复杂度

1. 渐进空间复杂度
2. 表示算法的存储空间与数据规模之间的增长关系

空间复杂度计算方法与时间复杂度类似

总结