归并排序和快速排序都用到了分治思想
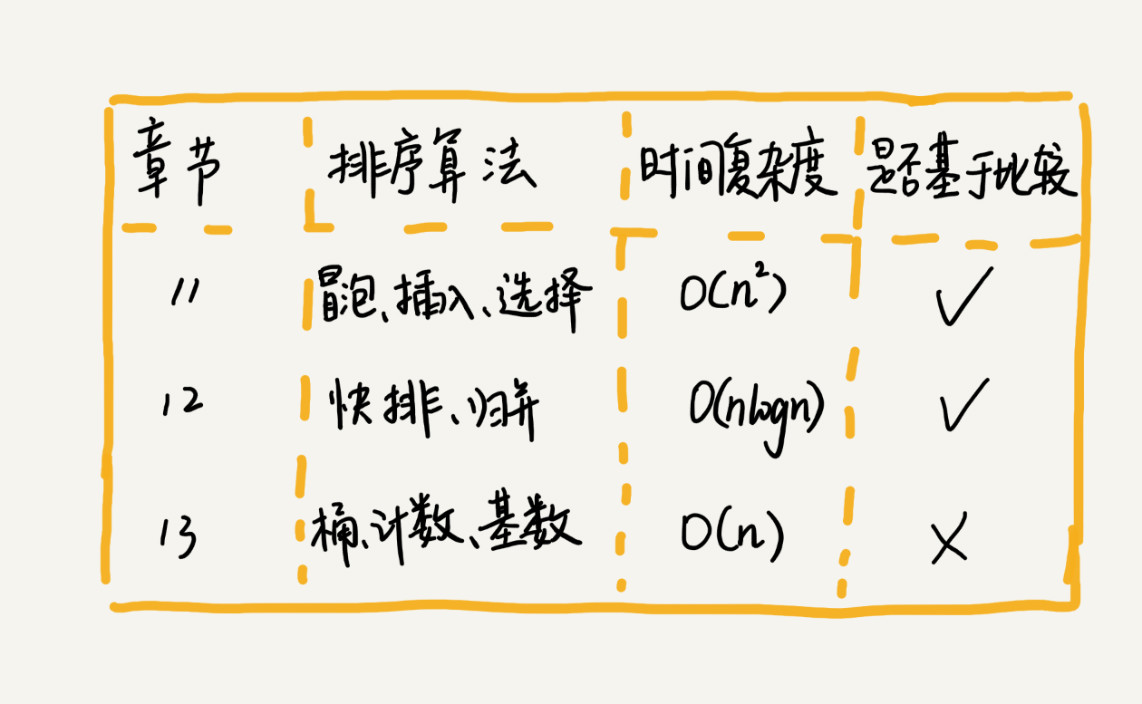
排序算法有很多,主要按时间复杂度分为三大类
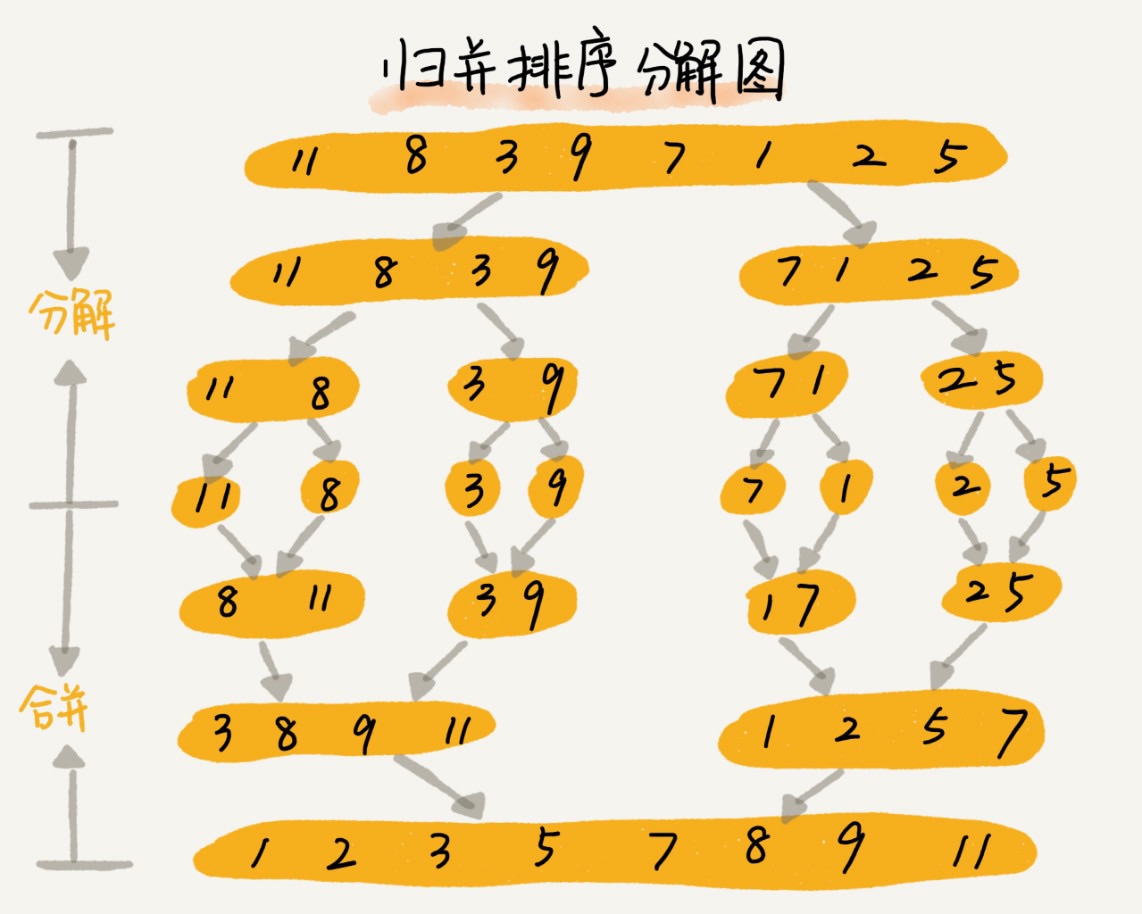
归并排序(Merge Sort)
算法
- 将数组以中点为分界点,分为两组
- 不断分解,直到每组只有一个元素
- 然后进行合并,在合并时,按大小一次合入
- 合入后的分组内的数据是有序的
- 以此向上回归,直到所有分组都合入一个
代码
- 伪代码
递推公式:
merge_sort(begin, end) = merge(merge_sort(begin, mid), merge_sort(mid+1, end))
终止条件:
p >= r 不用再继续分解- C++代码
void Sort::MergeSort(int data[], int length) { cout << "MergeSort:" << ToString(data, length) << endl; MergeSortC(data, 0, length - 1); cout << "MergeSort Result:" << ToString(data, length) << endl; } void Sort::MergeSortC(int data[], int begin, int end) { if (begin >= end) return; int mid = (begin + end) / 2; MergeSortC(data, begin, mid); MergeSortC(data, mid + 1, end); Merge(data, begin, mid, mid + 1 ,end); } void Sort::Merge(int data[], int begin1, int end1, int begin2, int end2) { // 打印排序过程 // for (int i = begin1; i <= end1; i++) { // if (i == end1) { // printf("+%d|", data[i]); // } else { // printf("+%d,", data[i]); // } // } // for (int i = begin2; i <= end2; i++) { // printf("-%d", data[i]); // } // printf("\n"); int i = begin1; int j = begin2; int length = end2 - begin1 + 1; int *tempData = new int[length]; int k = 0; while (i <= end1 && j <= end2) { if (data[i] <= data[j]) { tempData[k++] = data[i++]; } else { tempData[k++] = data[j++]; } } //判断哪个子数组中有剩余的数据 int start = i, end = end1; if (j <= end2) { start = j; end = end2; } //将剩余的数据拷贝到临时数组tempData中 while (start <= end) { tempData[k++] = data[start++]; } //将tempData中的数组拷贝会data中 for (int i = 0; i <= end2 - begin1; i++) { data[begin1+i] = tempData[i]; } delete tempData; }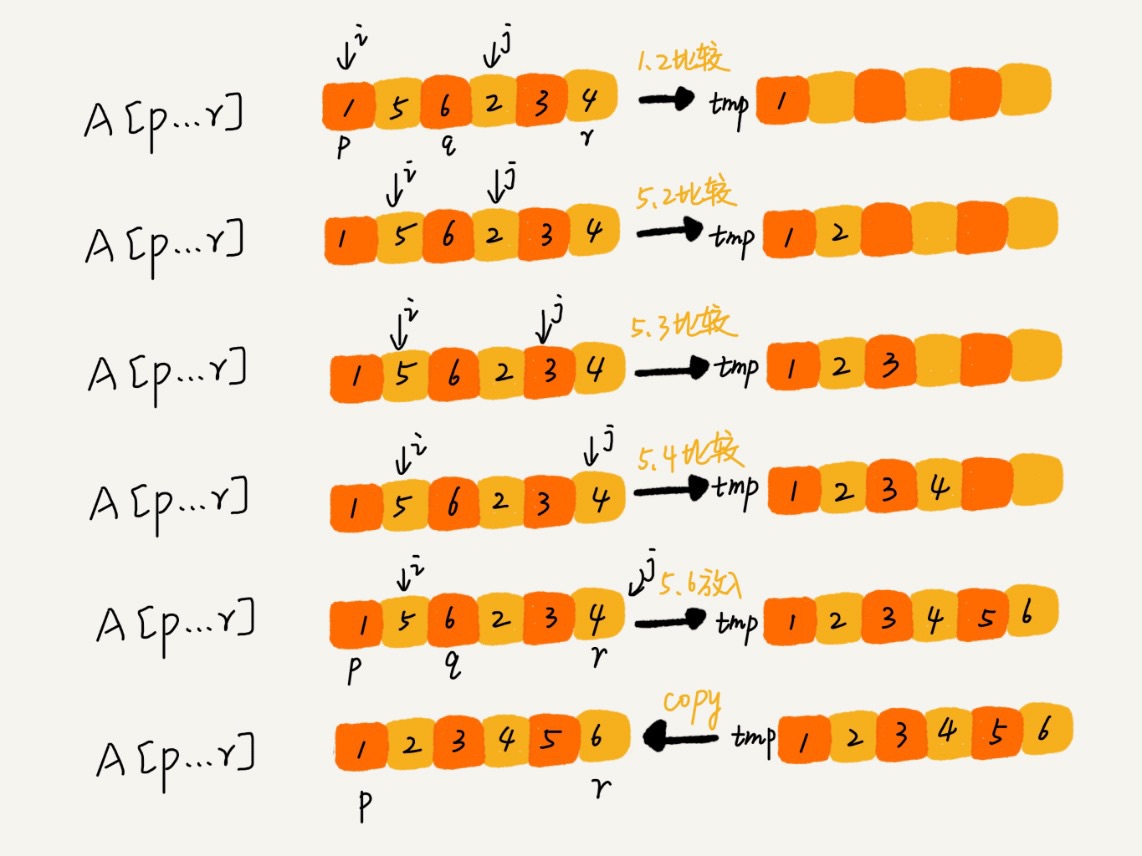
特性
- 稳定排序
- 时间复杂度O(nlogn)
- 空间复杂度O(n)
归并排序(Merge Sort)
算法
- 选择一个分割数,默认为数组最后一个
- 创建一个快索引和一个慢索引
- 每次快索引与分割数比较后向后移动一位
- 如果快索引小于分割数(符合条件),与慢索引互换位置,慢索引向后移动一位
- 最后将慢索引位置与分割数互换
- 等到左边小于分割数,右边大于分割数的数组
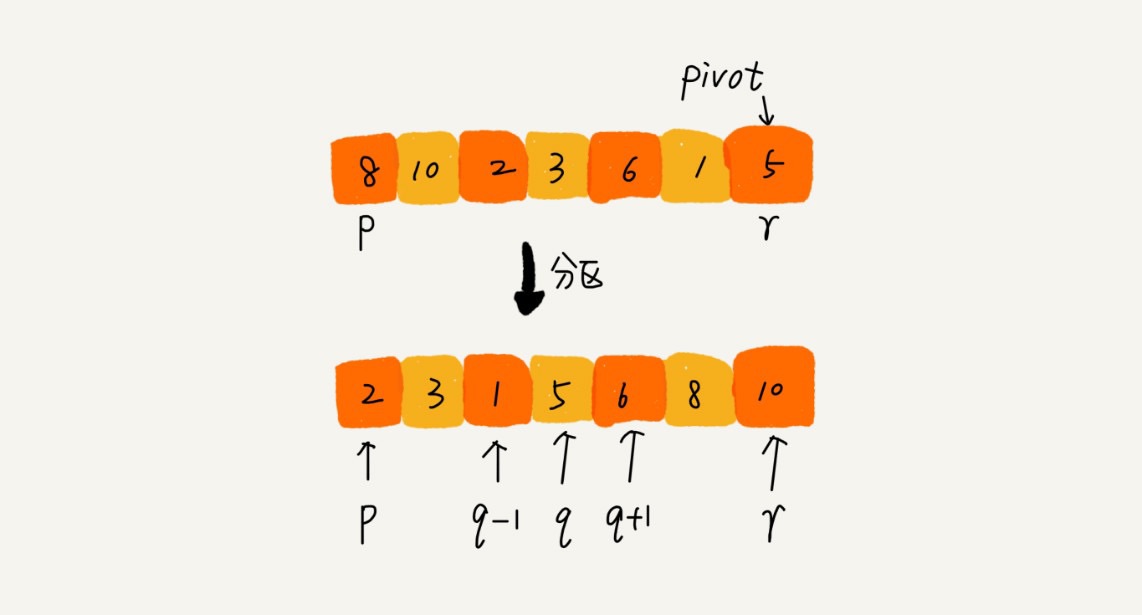
代码
- 伪代码
递推公式:
quick_sort(begin, end) = quick_sort(begin, partitionIndex - 1) + quick_sort(partitionIndex + 1, end)
终止条件:
begin >= end- C++代码
void Sort::QuickSort(int data[], int length) {
cout << "QuickSort:" << ToString(data, length) << endl;
QuickSortC(data, 0, length - 1);
cout << "QuickSort Result:" << ToString(data, length) << endl;
}
void Sort::QuickSortC(int data[], int begin, int end) {
if (begin >= end) return;
int partitionIndex = Partition(data, begin, end);
QuickSortC(data, begin, partitionIndex - 1);
QuickSortC(data, partitionIndex + 1, end);
}
int Sort::Partition(int data[], int begin, int end) {
int i = begin;
int pivot = data[end];
for (int j = begin; j < end; j++) {
if (data[j] < pivot) {
if (i != j) {
int tmp = data[i];
data[i] = data[j];
data[j] = tmp;
}
i++;
}
}
if (i != end) {
int tmp = data[i];
data[i] = data[end];
data[end] = tmp;
}
return i;
}- 简单:多创建一个数组用于用于数组排序,类似于归并排序
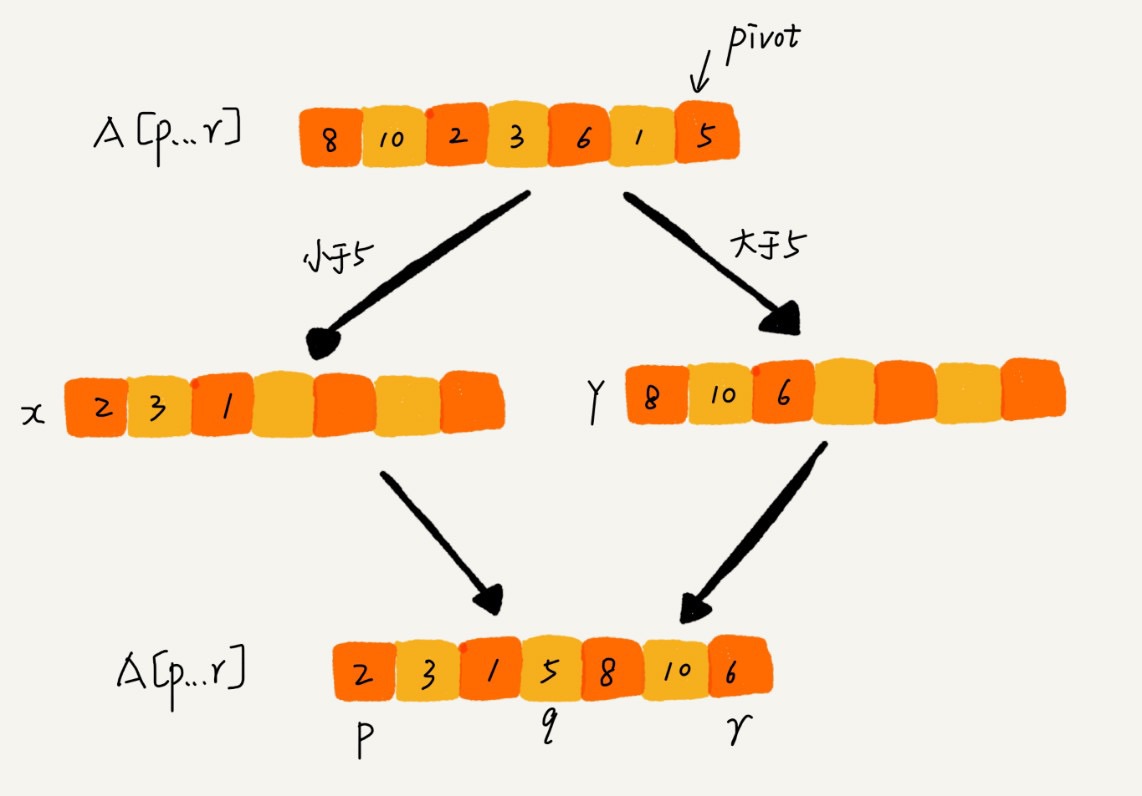
- 高级:使用快慢索引在原地排序
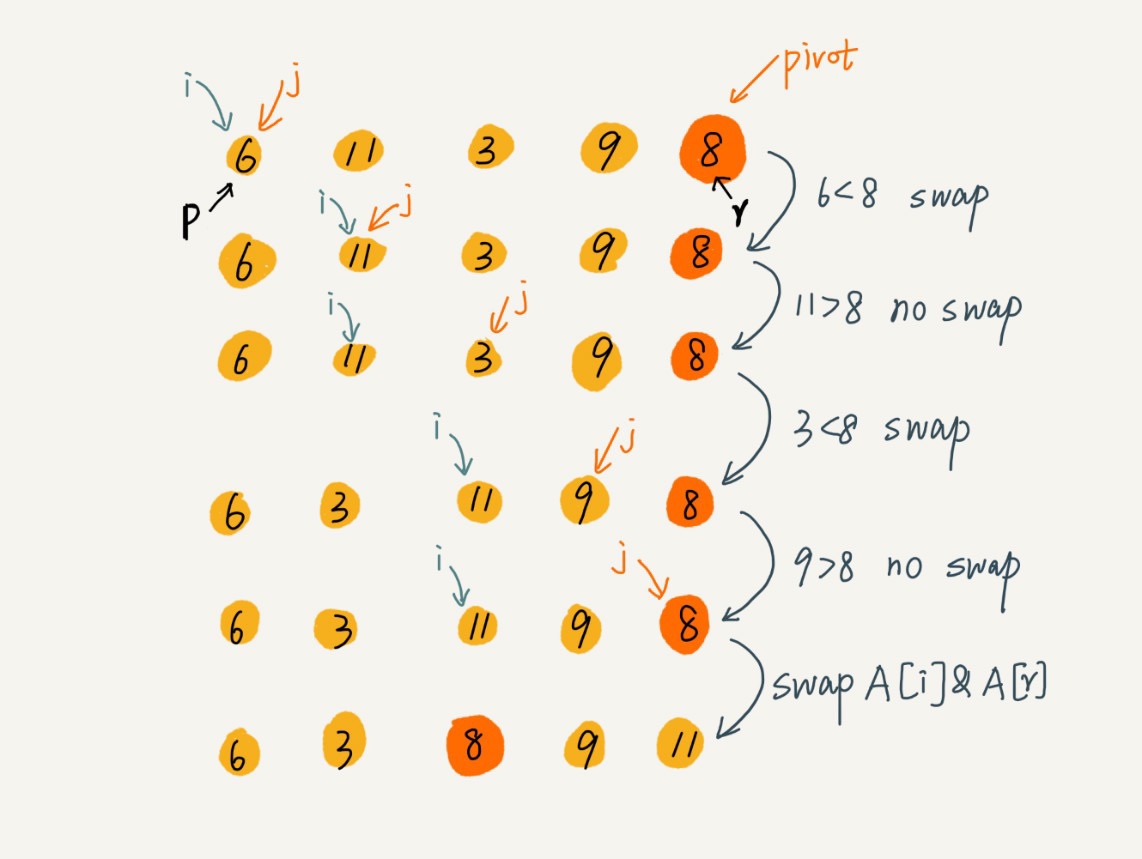
特性
- 不稳定排序
- 时间复杂度O(nlogn)
- 空间复杂度O(n)
归并排序 vs 快速排序
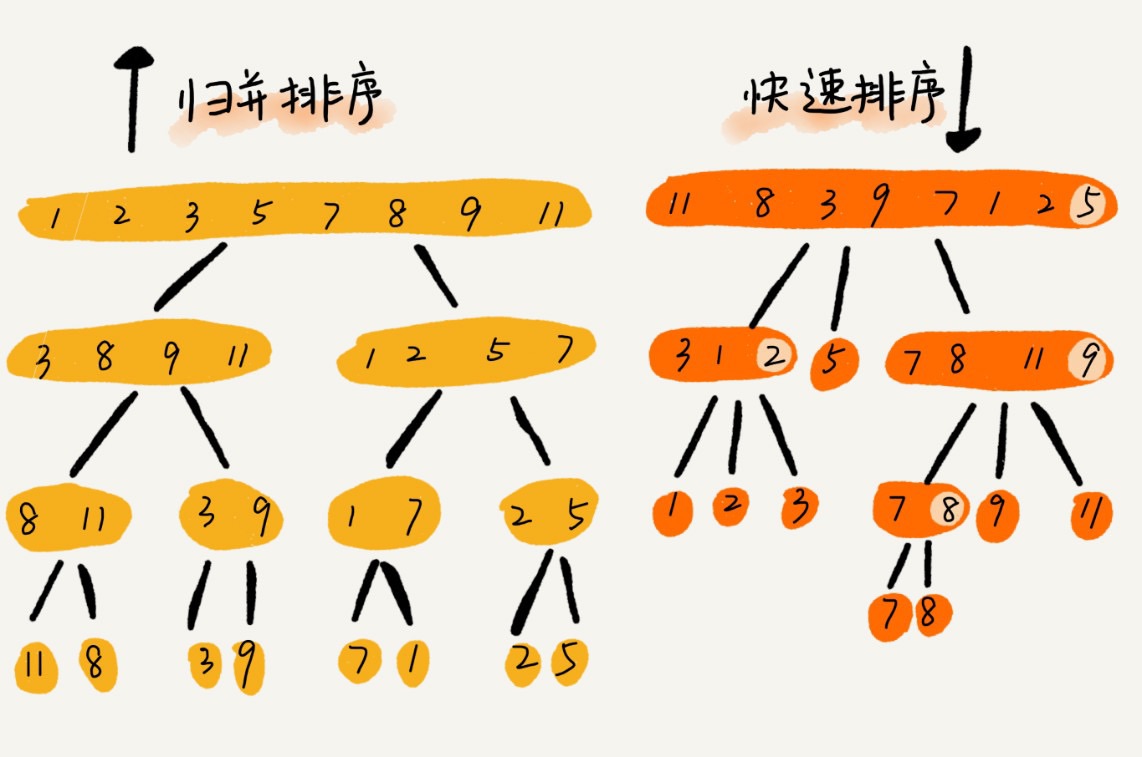
总结
- 都是分治思想
- 归并排序时间复杂度和数据内容无关,而快速排序和索取的partition的值有关
- 归并排序不是原地排序,而快速排序是原地排序
